オイラー 18世紀の天才数学者 解析学 サイクロプスとは 遺産と影響

Euler: The Genius Mathematician of the 18th Century – Analysis, Cyclops, Legacy, and Influence
イントロダクション
18世紀を代表する天才数学者、レオンハルト・オイラーは、その名を聞くだけで多くの数学者が敬意を払う存在です。
彼の業績は解析学をはじめ、数理物理学、天文学、工学など多岐にわたります。
オイラーの業績の中でも特に有名なのが、解析学の基礎を築いたことです。
彼が導入した記号や概念は、現代の数学でも頻繁に使用されています。
Introduction
Leonhard Euler, the prodigious mathematician of the 18th century, is a name that commands respect among mathematicians worldwide.
His contributions span a wide range of fields, including analysis, mathematical physics, astronomy, and engineering.
Among Euler’s many achievements, one of the most renowned is his foundational work in the field of analysis.
The symbols and concepts he introduced continue to be extensively used in modern mathematics.

A Cyclops: The Exceptional One-Eyed Giant with Remarkable Smithing Skills in Greek Mythology
また、オイラーは「サイクロプス」とも呼ばれるほどの視力の問題を抱えながらも、その知的探求心を止めることはありませんでした。
彼の視力は次第に悪化し、最終的には完全に失明しましたが、その後も驚異的なペースで研究を続け、数々の論文を執筆しました。オイラーの遺産と影響は、彼の死後も数学界に深く刻まれ続けています。
この記事では、オイラーの生涯と業績、そして彼が残した遺産とその影響について詳しく掘り下げていきます。
彼の功績がどのように現代の数学や科学に影響を与えたのか、その真髄を探ってみましょう。
Furthermore, Euler, despite facing visual impairments so severe that he was sometimes referred to as the “Cyclops,” never allowed his intellectual curiosity to wane.
His eyesight deteriorated over time, eventually leading to complete blindness. Yet, even then, he continued his research at an astonishing pace, producing numerous papers. Euler’s legacy and influence remain deeply ingrained in the mathematical community long after his passing.
This article delves into Euler’s life, accomplishments, and the legacy he left behind, exploring in detail how his contributions have impacted modern mathematics and science.
Let’s delve into the essence of how his achievements have shaped contemporary mathematics and science.
レオンハルト・オイラー:18世紀の数学者・天文学者の紹介
レオンハルト・オイラーは、18世紀を代表する「数学者・天文学者」です。
彼の業績は広範囲にわたり、特に「解析学」において重要な貢献をしました。
1707年にスイスのバーゼルで生まれたオイラーは、数学の天才として早くからその才能を発揮しました。
彼は「数学のサイクロプス(単眼の巨人)」とも称され、その卓越した計算能力と洞察力で知られています。
オイラーは、数学の基礎を築く多くの定理や公式を発見しました。
Introduction to Leonhard Euler: Mathematician and Astronomer of the 18th Century
Leonhard Euler stands as a prominent figure in the 18th century, known for his contributions as a mathematician and astronomer.
His achievements span a wide range, with particularly significant contributions in the field of analysis.
Born in Basel, Switzerland in 1707, Euler demonstrated his mathematical genius from an early age.
Referred to as the “mathematical Cyclops,” he was renowned for his exceptional computational skills and insight.
Euler discovered numerous theorems and formulas that laid the groundwork for mathematics.
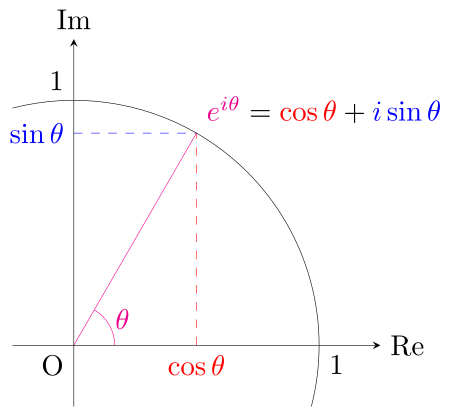
In the complex plane, the complex number ( e^{i\theta} ) represents a point on the unit circle with an angle ( \theta ) [rad].
例えば、オイラーの公式 (e^{i\pi} + 1 = 0) は数学史上最も美しい方程式の一つとされています。
また、彼は「グラフ理論」の創始者としても知られ、ケーニヒスベルクの橋の問題を解決する過程でこの理論を確立しました。
さらに、オイラーは天文学の分野でも多大な貢献を果たしました。
彼の研究は惑星の運動や月の軌道に関する理解を深め、当時の天文学の発展に寄与しました。
彼の業績は、現代の数学や科学の基盤を築く上で欠かせないものであり、その影響は今なお続いています。
オイラーの生涯とその功績
レオンハルト・オイラーは、1707年にスイスのバーゼルで生まれた「18世紀の数学者・天文学者」でした。
彼の父親も数学者であり、幼少期から数学に触れる環境にありました。
オイラーはバーゼル大学で学び、わずか13歳で学士号を取得するという驚異的な才能を示しました。
彼の功績の一つに「解析学」の発展があります。
オイラーは微分積分学の基礎を築き、数多くの定理を証明しました。特に「オイラーの公式」(e^{i\pi} + 1 = 0)は、数学の美しさを象徴する方程式として広く知られています。
また、オイラーは数学だけでなく、天文学や物理学、工学など多岐にわたる分野で業績を残しました。
彼の著作は膨大で、数千ページにも及ぶ論文を執筆しました。
そのため、オイラーは「数学のサイクロプス(単眼の巨人)」と称されることもあります。
晩年には視力を失いましたが、それでもなお数学の研究を続け、多くの弟子を育てました。
1783年に76歳で亡くなるまで、オイラーの情熱は衰えることがありませんでした。
彼の影響は現代の数学にも色濃く残っており、その功績は永遠に語り継がれるでしょう。
Furthermore, he is credited as the founder of “Graph Theory,” having established this theory while resolving the Seven Bridges of Königsberg problem.
Moreover, Euler made significant contributions in the field of astronomy.
His research deepened the understanding of planetary motion and lunar orbits, contributing to the advancement of astronomy during his time.
His accomplishments are indispensable in laying the foundation of modern mathematics and science, and his influence continues to endure.
The Life and Achievements of Leonhard Euler
Leonhard Euler, born in Basel, Switzerland in 1707, was an “18th-century mathematician and astronomer.”
Growing up in an environment where mathematics was prevalent due to his father’s own profession as a mathematician, Euler displayed remarkable talent from an early age.
Studying at the University of Basel, he demonstrated extraordinary ability by earning a bachelor’s degree at the remarkable age of 13.
Among his many achievements is the development of “Analysis.”
Euler laid the groundwork for calculus, proving numerous theorems. Particularly, “Euler’s formula” (( e^{i\pi} + 1 = 0 )) is widely known as a symbol of mathematical beauty.
Additionally, Euler left his mark not only in mathematics but also in diverse fields such as astronomy, physics, and engineering.
His extensive body of work includes writing thousands of pages of papers.
Hence, Euler is sometimes referred to as the “mathematical Cyclops” due to his prolific output.
Despite losing his eyesight in his later years, he continued his mathematical research and mentored many disciples.
Euler’s passion remained unwavering until his death at the age of 76 in 1783.
His influence strongly persists in modern mathematics, and his achievements will be forever remembered.
オイラーと解析学:数学のサイクロプス(単眼の巨人)としての役割
レオンハルト・オイラーは18世紀の数学者・天文学者として知られ、解析学の発展に大きく貢献した人物です。
彼の業績は多岐にわたり、特に「オイラーの公式」や「オイラーの定理」は数学の基礎を築き上げました。
オイラーは視力を失った後も、驚異的な計算能力を発揮し続け、「数学のサイクロプス(単眼の巨人)」と称されました。
オイラーの解析学への貢献は、微分積分学の発展においても重要です。
彼は関数の概念を拡張し、無限級数や微分方程式の理論を深化させました。
彼の著作『Introductio in analysin infinitorum』は、解析学の基礎となる重要な文献です。
また、オイラーはグラフ理論の創始者でもあり、ケーニヒスベルクの橋問題を解決したことで知られます。
この問題は、現代のネットワーク理論の先駆けとなりました。
オイラーの影響は数学だけでなく、物理学や工学など多岐にわたります。
彼の業績は、今なお多くの研究者に影響を与え続けています。
Euler and Analysis: The Role of a Mathematical Cyclops
Leonhard Euler is renowned as an 18th-century mathematician and astronomer who made significant contributions to the development of analysis.
His achievements span various areas, notably establishing the foundations of mathematics with “Euler’s formula” and “Euler’s theorem.”
Even after losing his eyesight, Euler continued to display remarkable computational abilities, earning him the moniker “mathematical Cyclops.”
Euler’s contributions to analysis are crucial, particularly in the advancement of calculus.
He expanded the concept of functions and deepened the theories of infinite series and differential equations.
His work “Introductio in analysin infinitorum” stands as a seminal text in the foundation of analysis.
Additionally, Euler is credited as the founder of graph theory, known for solving the Seven Bridges of Königsberg problem, a precursor to modern network theory.
Euler’s influence extends beyond mathematics into physics, engineering, and other fields.
His achievements continue to inspire countless researchers to this day.
オイラーの業績:数学と天文学への貢献
18世紀の数学者・天文学者であるレオンハルト・オイラーは、「数学のサイクロプス(単眼の巨人)」とも称されるほどの偉業を成し遂げた。
彼の解析学への貢献は特筆すべきもので、オイラーの公式やオイラーの定数など、多くの基本的な概念を提唱した。
特に、オイラーの公式は複素解析において不可欠なもので、数学の基礎を大きく進展させた。
また、オイラーは天文学の分野でも多大な貢献をしている。
彼の研究は、惑星の運動や軌道計算において重要な役割を果たした。
オイラー法と呼ばれる数値解析の手法は、天体の軌道を計算する際に用いられ、現在でも広く活用されている。
彼の業績は、数学と天文学の双方において、後世の研究者たちに多大な影響を与え続けている。
オイラーの多岐にわたる研究は、現代の科学技術の基盤を築く上で欠かせないものとなっている。
“Euler’s Contributions: Advancements in Mathematics and Astronomy”
Leonhard Euler, an 18th-century mathematician and astronomer, achieved remarkable feats, often referred to as the “Cyclops of Mathematics” due to his monumental contributions.
His contributions to calculus are noteworthy, having proposed many fundamental concepts such as Euler’s formula and Euler’s constant.
Particularly, Euler’s formula is indispensable in complex analysis, significantly advancing the foundations of mathematics.
Moreover, Euler made significant contributions in the field of astronomy. His research played a crucial role in the study of planetary motion and orbit calculations.
The numerical analysis technique known as Euler’s method is widely used in calculating celestial orbits and remains prevalent today.
His achievements continue to profoundly influence researchers in both mathematics and astronomy, laying a crucial foundation for modern scientific and technological advancements.
オイラーの解析学への貢献
18世紀の数学者・天文学者であるレオンハルト・オイラーは、解析学において多大な貢献を果たしました。
彼は「数学のサイクロプス(単眼の巨人)」と称され、その名に恥じない業績を残しています。オイラーの功績の一つに、オイラーの公式 ( e^{i\pi} + 1 = 0 ) があります。
この公式は数学の美しさを象徴するもので、多くの数学者に影響を与えました。
また、オイラーは関数の概念を深化させ、微分積分学の発展に寄与しました。
彼の著書『Introductio in analysin infinitorum』(1748年)は、解析学の基礎を築いた重要な作品です。
この著書では、無限級数や三角関数の解析的な取り扱いが詳細に述べられています。
さらに、オイラーは「オイラー数」や「オイラー多面体定理」など、多くの数学的概念を導入しました。
これらの業績は、現代の数学研究においても不可欠な要素となっています。
オイラーの解析学への貢献は、彼の名を永遠に刻むものであり、数学史において燦然と輝く存在です。
“Euler’s Contributions to Analysis”
Leonhard Euler, an 18th-century mathematician and astronomer, made significant contributions to the field of analysis.
Dubbed the “Cyclops of Mathematics,” Euler left behind a legacy worthy of his name. One of his notable achievements is Euler’s formula ( e^{i\pi} + 1 = 0 ), which symbolizes the beauty of mathematics and has influenced many mathematicians.
Moreover, Euler deepened the concept of functions and contributed to the development of calculus.
His book “Introductio in analysin infinitorum” (1748) laid the foundation for analysis, detailing the analytical treatment of infinite series and trigonometric functions.
Additionally, Euler introduced many mathematical concepts such as “Euler numbers” and “Euler’s polyhedron theorem.”
These contributions remain indispensable elements in contemporary mathematical research.
Euler’s contributions to analysis immortalize his name, making him a radiant figure in the history of mathematics.
他の数学分野への貢献:数論、幾何学、数理物理学
18世紀の数学者・天文学者であるレオンハルト・オイラーは、その多岐にわたる業績で数学と天文学の歴史に輝かしい足跡を残しました。
彼の貢献は一つの分野にとどまらず、数論、幾何学、数理物理学と広範囲にわたります。
オイラーの業績は「数学のサイクロプス(単眼の巨人)」と称されるほどで、その影響力は現在でも色褪せることがありません。
解析学におけるオイラーの業績
解析学の分野でオイラーが成し遂げた業績は特に有名です。
彼の公式 (e^{i\pi} + 1 = 0) は「オイラーの公式」として広く知られ、数学の美しさを象徴するものとされています。
この公式は、自然対数の底 (e)、虚数単位 (i)、円周率 (\pi)、そして基本的な数 (1) と (0) を一つの等式に結びつけるもので、数学者にとってはまさに芸術作品です。
数論とオイラーのトーシェント関数
数論においても、オイラーの貢献は計り知れません。
彼はオイラーのトーシェント関数 (\phi(n)) を導入し、これが素数の性質を研究する上で重要な役割を果たしました。
この関数は、ある数 (n) 以下の自然数の中で (n) と互いに素である数の個数を表します。
オイラーのトーシェント関数は、フェルマーの小定理やオイラーの定理など、多くの重要な数学的結果に応用されています。
幾何学とオイラーの多面体定理
幾何学の分野でも、オイラーは重要な発見をしています。
特に有名なのがオイラーの多面体定理です。
この定理は、任意の凸多面体において、頂点の数 (V)、辺の数 (E)、および面の数 (F) の間に (V – E + F = 2) という関係が成り立つことを示しています。
この公式は、多面体の基本的な性質を理解する上で欠かせないものであり、数学教育の基礎として広く教えられています。
数理物理学とオイラーの方程式
数理物理学の分野でも、オイラーの業績は目を見張るものがあります。
彼は流体力学における重要な方程式を導出し、これが後の研究に大きな影響を与えました。
特に有名なのがオイラーの流体方程式で、これは非圧縮性流体の運動を記述する基本的な方程式です。
また、天文学においてもオイラーは多くの貢献をしており、彼の研究はニュートン力学の発展に大きく寄与しました。
“Euler’s Contributions to Other Fields of Mathematics: Number Theory, Geometry, and Mathematical Physics”
Leonhard Euler, an 18th-century mathematician and astronomer, left illustrious footprints in the history of mathematics and astronomy through his diverse achievements.
His contributions extended beyond a single field, spanning number theory, geometry, and mathematical physics.
Euler’s achievements are so significant that he is often dubbed the “Cyclops of Mathematics,” and his influence remains undiminished today.
Euler’s Contributions in Analysis
Euler’s accomplishments in the field of analysis are particularly renowned.
His formula (e^{i\pi} + 1 = 0), known as “Euler’s formula,” is widely recognized, symbolizing the beauty of mathematics. It elegantly ties together the natural logarithm base (e), the imaginary unit (i), the constant pi ((\pi)), and the fundamental numbers 1 and 0 into a single equation, akin to a work of art for mathematicians.
Number Theory and Euler’s Totient Function
In number theory, Euler’s contributions are immeasurable.
He introduced Euler’s totient function (\phi(n)), which played a crucial role in studying the properties of prime numbers. This function represents the count of numbers less than or equal to (n) that are coprime to (n).
Euler’s totient function has been applied to many significant mathematical results, including Fermat’s little theorem and Euler’s theorem.
Geometry and Euler’s Polyhedron Theorem
In the field of geometry, Euler made significant discoveries.
One of his most famous contributions is Euler’s polyhedron theorem, which states that for any convex polyhedron, the number of vertices ((V)), edges ((E)), and faces ((F)) satisfies the relationship (V – E + F = 2). This formula is essential for understanding the basic properties of polyhedra and is widely taught as part of mathematics education.
Mathematical Physics and Euler’s Equations
Euler’s contributions in the field of mathematical physics are remarkable.
He derived important equations in fluid dynamics that had a profound impact on subsequent research. Particularly notable is Euler’s fluid equation, which describes the motion of incompressible fluids and serves as a fundamental equation in the field.
Additionally, Euler made significant contributions to astronomy, greatly influencing the development of Newtonian mechanics.
Euler’s legacy in various mathematical fields remains a beacon of inspiration for mathematicians and scientists alike.
オイラーの遺産
レオンハルト・オイラーの業績は、彼が「数学のサイクロプス(単眼の巨人)」と称される理由を物語っています。
彼の研究は多くの数学者にとってインスピレーションの源であり、現代の数学や科学の基礎を築く上で欠かせないものでした。
オイラーの多岐にわたる貢献は、今後も長く語り継がれることでしょう。
“Euler’s Legacy”
The achievements of Leonhard Euler paint a picture of why he’s often referred to as the “Cyclops of Mathematics.”
His research served as a wellspring of inspiration for many mathematicians and laid an indispensable foundation for modern mathematics and science.
Euler’s diverse contributions are sure to be celebrated and passed down for generations to come.
関数概念の導入とその影響
オイラーの関数概念の革新
18世紀の数学者・天文学者であるレオンハルト・オイラーは、数学の世界に多大な影響を与えた人物です。
彼は「数学のサイクロプス(単眼の巨人)」と称されるほど、その知識と業績が際立っていました。
特に、関数概念の発展においてオイラーの功績は絶大です。
オイラーは関数を形式的に定義し、解析学の基盤を築きました。
彼の定義によって、関数は単なる数値の集合ではなく、数値間の関係を示す重要なツールとなりました。
この革新により、微積分や微分方程式の理論が飛躍的に進展しました。
微積分と微分方程式への貢献
オイラーの関数概念は、微積分の発展においても重要な役割を果たしました。
微積分は、物理学や工学など多くの分野で不可欠な数学的手法です。
オイラーは微分方程式の解法を体系化し、その理論を確立しました。
例えば、オイラーの方法と呼ばれる数値解析の手法は、今日でも広く用いられています。
さらに、オイラーは円周率(π)や自然対数の底(e)といった数学定数の研究にも尽力しました。
彼の公式や定理は、現代の数学教育においても基礎的な知識として教えられています。
教育と科学技術への影響
オイラーの業績は、数学教育にも大きな影響を与えました。
彼の著作は多くの教科書に取り入れられ、数学の基礎として広く学ばれています。
オイラーの名前は、数学を学ぶ学生にとって馴染み深いものとなっています。
また、オイラーの研究は科学技術の発展にも寄与しました。
彼の理論は、物理学や工学、情報科学など多岐にわたる分野で応用されています。
例えば、オイラーの多面体定理は、コンピュータグラフィックスや建築設計においても重要な役割を果たしています。
オイラーの遺産
レオンハルト・オイラーの業績は、数学の枠を超えて広がっています。
彼の関数概念の革新は、数学の発展にとって不可欠な要素となり、現代の科学技術にも大きな影響を与えています。
オイラーの名前は、今後も数学の歴史において輝き続けることでしょう。
“The Introduction of Function Concept and Its Impact”
“Euler’s Innovative Concept of Functions”
Leonhard Euler, an 18th-century mathematician and astronomer, left an indelible mark on the world of mathematics.
His knowledge and achievements were so outstanding that he earned the title of the “Cyclops of Mathematics.”
Particularly noteworthy is Euler’s monumental contribution to the development of the concept of functions.
Euler formally defined functions, laying the groundwork for the field of analysis.
His definition transformed functions from mere collections of numbers to essential tools illustrating relationships between numerical values.
This innovation led to significant advancements in the theories of calculus and differential equations.
“Contributions to Calculus and Differential Equations”
Euler’s concept of functions played a crucial role in the development of calculus.
Calculus is an indispensable mathematical technique in fields such as physics and engineering.
Euler systematized methods for solving differential equations, establishing their theory.
For instance, numerical analysis techniques known as Euler’s methods are widely used even today.
Furthermore, Euler dedicated efforts to studying mathematical constants like pi (π) and the base of natural logarithms (e).
His formulas and theorems are taught as fundamental knowledge in modern mathematical education.
“Impact on Education and Scientific Technology”
Euler’s achievements significantly influenced mathematics education.
His works have been incorporated into numerous textbooks and are widely studied as the foundation of mathematics.
The name Euler is familiar to students learning mathematics.
Moreover, Euler’s research contributed to advancements in scientific technology.
His theories have applications in various fields such as physics, engineering, and computer science.
For example, Euler’s polyhedron theorem plays a crucial role in computer graphics and architectural design.
“Euler’s Legacy”
The legacy of Leonhard Euler extends beyond the realm of mathematics.
His innovative concept of functions became an indispensable element in the development of mathematics and had a profound impact on modern scientific technology.
The name Euler will continue to shine brightly in the history of mathematics for years to come.
オイラーの人生:数学者としての道のり
レオンハルト・オイラーは1707年にスイスのバーゼルで生まれた。
彼は18世紀を代表する数学者・天文学者であり、その業績は数学界に多大な影響を与えた。
オイラーは「数学のサイクロプス(単眼の巨人)」とも称され、視力を失ってもなお数多くの論文を執筆し続けた。
彼の代表的な業績の一つに「解析学」の発展がある。
オイラーは微分方程式や無限級数などの分野で画期的な成果を挙げた。
例えば、オイラーの公式 ( e^{ix} = \cos(x) + i\sin(x) ) は、複素解析における基本定理として知られている。
また、オイラーはグラフ理論の創始者としても知られる。
ケーニヒスベルクの橋の問題を解決する過程で、彼はグラフの概念を導入し、これが後のネットワーク理論の基礎となった。
オイラーの業績は数学だけでなく、物理学や工学にも及び、彼の名前を冠した定理や公式は数多く存在する。
彼の生涯を通じての貢献は、まさに「数学のサイクロプス」としての名にふさわしいものであった。
“Euler’s Life: The Journey of a Mathematician”
Leonhard Euler was born in Basel, Switzerland, in 1707.
He became one of the most prominent mathematicians and astronomers of the 18th century, leaving a profound impact on the world of mathematics.
Euler was often referred to as the “Cyclops of Mathematics” and continued to write numerous papers even after losing his sight.
One of his significant achievements lies in the development of “analysis.”
Euler made groundbreaking contributions in fields like differential equations and infinite series.
For instance, Euler’s formula (e^{ix} = \cos(x) + i\sin(x)) is renowned as a fundamental theorem in complex analysis.
Moreover, Euler is recognized as a pioneer in graph theory.
In solving the Königsberg Bridge problem, he introduced the concept of graphs, laying the groundwork for later network theory.
Euler’s contributions extended beyond mathematics into physics and engineering, with many theorems and formulas bearing his name.
His lifelong contributions truly lived up to the title of the “Cyclops of Mathematics.”
オイラーの著作:数学界に残した遺産
レオンハルト・オイラーは18世紀の偉大な数学者・天文学者であり、彼の業績は現代数学に多大な影響を与えています。
オイラーは「数学のサイクロプス(単眼の巨人)」と称されるほどの天才で、解析学の発展において重要な役割を果たしました。
彼の著作には『無限小解析入門』や『解析学講義』などがあり、これらの作品は数学の基礎を築く上で欠かせないものです。
また、オイラーはオイラーの公式やオイラーの定理など、多くの重要な数学的概念を提唱しました。
彼の研究は数論、幾何学、物理学など多岐にわたり、その影響は今日でも続いています。
特に、オイラーの公式は複素数の解析において基本的な役割を果たし、数学の美しさを象徴するものとされています。
オイラーの知識は数学界において不滅の遺産となり、彼の著作は今でも多くの研究者や学生にとって重要な参考資料です。
オイラーの業績は、数学の歴史において輝かしい一ページを飾っています。
“Euler’s Works: The Legacy Left in the Mathematical World”
Leonhard Euler, a great mathematician and astronomer of the 18th century, has had a profound influence on modern mathematics.
Euler was hailed as the “Cyclops of Mathematics,” showcasing his genius and playing a crucial role in the development of analysis.
His works include “Introduction to the Analysis of the Infinite” and “Lectures on Analysis,” foundational pieces in the world of mathematics.
Moreover, Euler proposed many significant mathematical concepts like Euler’s formula and Euler’s theorem.
His research spanned various fields such as number theory, geometry, and physics, and its impact persists today.
In particular, Euler’s formula plays a fundamental role in the analysis of complex numbers, symbolizing the beauty of mathematics.
Euler’s knowledge stands as an enduring legacy in the mathematical world, and his works remain vital references for many researchers and students.
Euler’s achievements adorn a brilliant page in the history of mathematics.
関連項目:オイラーと関連する主要なトピック
レオンハルト・オイラー:18世紀の数学界の巨人オンハルト・オイラーは、18世紀を代表する数学者・天文学者として知られています。
彼の業績は非常に多岐にわたり、その影響力は現代の数学にまで及んでいます。
彼は「数学のサイクロプス(単眼の巨人)」とも称され、その名に恥じない数々の偉業を成し遂げました。
解析学の革新者
オイラーは解析学の分野で特に大きな貢献をしました。
彼が導入した「オイラーの公式」e^(iπ) + 1 = 0は、数学界で最も美しい公式とされています。
この公式は、自然対数の底e、虚数単位i、円周率π、そして1と0という異なる数学的概念を一つの式に結びつけています。
この驚異的な統一性は、数学者のみならず多くの科学者にも感銘を与えました。
オイラーの多面体定理
オイラーの多面体定理もまた、彼の業績の一つとして知られています。
この定理は、任意の凸多面体において、頂点の数V、辺の数E、面の数Fが次の関係式を満たすことを示しています:V – E + F = 2。
このシンプルな関係式は、幾何学の基本的な性質を理解する上で非常に重要です。
ベータ関数とガンマ関数の研究
オイラーはまた、ベータ関数やガンマ関数の研究にも多大な貢献をしました。
ベータ関数は、積分を用いて定義される特別な関数であり、ガンマ関数は階乗の一般化として知られています。
これらの関数は、解析学や統計学、物理学など多くの分野で重要な役割を果たしています。
18世紀の数学者・天文学者としての影響
レオンハルト・オイラーの影響力は、18世紀にとどまらず現代にまで続いています。
彼の研究は、数学の発展において計り知れない影響を与え、多くの研究者にインスピレーションを提供しています。
オイラーの業績は、数学の基礎を築き、解析学を革新し、幾何学の理解を深め、特別な関数の研究を推進しました。
Related Topics: Key Areas Associated with Euler
Leonhard Euler: The Giant of the 18th-Century Mathematical World
Leonhard Euler is renowned as one of the most prominent mathematicians and astronomers of the 18th century, leaving a profound legacy that extends to modern mathematics.
His contributions were vast and far-reaching, influencing contemporary mathematical thought.
He is often referred to as the “Cyclops of Mathematics,” a fitting moniker for the numerous remarkable achievements he made.
Innovator of Analysis
Euler made significant contributions in the field of analysis.
His introduction of “Euler’s formula” (e^{i\pi} + 1 = 0) is considered one of the most beautiful equations in mathematics.
This formula elegantly ties together disparate mathematical concepts such as the base of natural logarithms (e), the imaginary unit (i), the constant (\pi), and the numbers 1 and 0.
This remarkable unity has impressed not only mathematicians but also many scientists.
Euler’s Polyhedral Theorem
Euler’s Polyhedral Theorem is another well-known accomplishment of his.
This theorem states that for any convex polyhedron, the number of vertices (V), edges (E), and faces (F) satisfy the equation: (V – E + F = 2).
This simple relationship is crucial for understanding the fundamental properties of geometry.
Research on Beta and Gamma Functions
Euler also made significant contributions to the study of beta and gamma functions.
The beta function, defined using integrals, and the gamma function, known as the generalization of factorials, play important roles in various fields such as analysis, statistics, and physics.
Influence as a Mathematician and Astronomer in the 18th Century
The influence of Leonhard Euler extends beyond the 18th century into the modern era.
His research has had immeasurable impact on the development of mathematics, inspiring countless researchers.
Euler’s achievements laid the foundation of mathematics, revolutionized analysis, deepened our understanding of geometry, and propelled the study of special functions.
最後に:オイラーの遺産の重要性
レオンハルト・オイラー:18世紀の数学者・天文学者、解析学の巨匠
数学のサイクロプス:レオンハルト・オイラーの生涯と業績
レオンハルト・オイラー(Leonhard Euler)は、1707年にスイスのバーゼルで生まれ、18世紀を代表する数学者・天文学者としてその名を歴史に刻みました。
彼は「数学のサイクロプス(単眼の巨人)」と称されるほどの天才であり、その業績は数学の基礎を築き上げるだけでなく、現代の科学技術にも深い影響を与えました。
オイラーの生涯を通じての功績を見ていきましょう。
オイラーの公式 ( e^{i\pi} + 1 = 0 ) とその美しさ
オイラーの公式 ( e^{i\pi} + 1 = 0 ) は、数学の美しさを象徴するものとして広く知られています。
この公式は、自然対数の底 ( e )、虚数単位 ( i )、円周率 ( \pi )、1、および0という数学の基本的な定数を一つの等式にまとめています。
この公式の美しさは、多くの数学者や科学者にとってインスピレーションの源となり、解析学の発展に大きく貢献しました。
数学の多岐にわたる貢献
レオンハルト・オイラーは、数多くの論文を執筆し、その総数は800を超えると言われています。
彼の研究は解析学、数論、幾何学、トポロジー、そして天文学など、数学の多くの分野にわたっています。
例えば、オイラーは多項式の根の分布に関する理論、グラフ理論の基礎、そしてオイラーの多面体公式 ( V – E + F = 2 ) など、多くの重要な概念を提唱しました。
これらの業績は、現代の数学研究においても重要な位置を占めています。
不屈の精神:視力を失っても続けた研究
レオンハルト・オイラーは、晩年に視力を失いましたが、それでも精力的に研究を続けました。
視力を失った後も、彼は数多くの論文を執筆し、その不屈の精神は多くの科学者にとってインスピレーションの源となりました。
彼の研究室には、多くの助手や学生が集まり、彼の指導の下で研究を進めました。
このようにして、オイラーの影響は彼自身の業績だけでなく、彼が育てた多くの弟子たちにも及びました。
未来永劫に生き続ける遺産
レオンハルト・オイラーの遺産は、数学の進化とともに未来永劫にわたって生き続けるでしょう。
彼の業績は、現代の数学や科学技術の基礎を築き上げ、その影響は今なお新たな発見や理論の中に息づいています。
オイラーの生涯と業績を知ることで、私たちは数学の美しさとその無限の可能性に改めて気づかされるのです。
In Conclusion: The Significance of Euler’s Legacy
Leonhard Euler: The Master of 18th-Century Mathematics and Astronomy
Leonhard Euler, born in Basel, Switzerland, in 1707, made his mark in history as a renowned mathematician and astronomer of the 18th century.
Renowned as the “Cyclops of Mathematics,” Euler’s brilliance not only laid the groundwork for mathematics but also profoundly influenced modern science and technology.
Let’s explore Euler’s achievements throughout his life.
Euler’s Formula ( ( e^{i\pi} + 1 = 0 ) ) and Its Beauty
Euler’s formula (( e^{i\pi} + 1 = 0 )) is widely celebrated for its elegance in representing fundamental mathematical constants—natural logarithm base ( ( e ) ), imaginary unit ( ( i ) ), pi ( ( \pi ) ), 1, and 0—in a single equation.
The beauty of this formula has inspired mathematicians and scientists alike, significantly contributing to the advancement of analysis.
Diverse Contributions to Mathematics
Leonhard Euler authored over 800 papers covering a wide array of mathematical fields, including analysis, number theory, geometry, topology, and astronomy.
For instance, Euler proposed groundbreaking theories on the distribution of polynomial roots, laid the foundation for graph theory, and introduced Euler’s polyhedral formula ( ( V – E + F = 2 ) ), among other pivotal concepts.
His contributions continue to hold a prominent place in contemporary mathematical research.
Indomitable Spirit: Continuing Research Despite Vision Loss
Despite losing his sight in his later years, Leonhard Euler continued his research with unwavering determination.
Even after losing his vision, he authored numerous papers, serving as a beacon of inspiration for countless scientists.
His research chamber was frequented by many assistants and students who continued their studies under his guidance, further extending Euler’s influence.
An Everlasting Legacy
Leonhard Euler’s legacy will endure for eternity, shaping the evolution of mathematics and science.
His contributions laid the foundation for modern mathematics and scientific technology, with his influence permeating through new discoveries and theories.
By understanding Euler’s life and achievements, we are reminded of the beauty of mathematics and its infinite possibilities.

Warning: Undefined variable $comment_form_sns_tags in /home/ktsky/philosophy-kayak.com/public_html/wp-content/themes/shaper/comments.php on line 27